Continuous Compounding

Continuous compounding is the mathematical method use to calculate interest in which the earning is reinvested over the endless number of period. It means that we invest the principal balance and receive interest in the first period and the interest will be reinvested in the second period. The interest from the second period will be invested in the next, and this cycle will continue to grow the earning.   It is almost impossible as the investment needs to have the start and ending time.

The period of compounding interest can be annual, quarterly, and semi-annual which depends on the term of deposit or investment.

The continuous compounding of interest lead to a significant growth if we compare with a normal compound interest.

Continuous Compounding Formula

We can’t calculate the continued compounding for the infinite time period, so this formula use when we know the exact period of time.

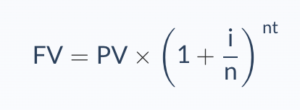
• PV = the present value of the investment or the principle
• i = interest rate
• n = the number of compounding periods
• t = the time in years

Continuous Compounding Example

For example, we decide to invest $ 100,000 and is expected to earn 12% per annum. However, we may end up with different if the interest is compounded base at different times. Please calculate the future value if the interest compound daily, monthly, and annually.

• Compound annually

FV = $ 100,000 * [1+ (12%/1)]^1*1 = $ 112,000

• Compound monthly

FV = $ 100,000 * [1+ (12%/12)]^ 12*1 = $ 112,683

• Compound daily

FV = $ 100,000 * [1+ (12%/365)]^365*1 = $ 112,747

Continuous Compounding Feature

• The interest earnings will be reinvested to earn more interest.
• The balance continues to earn and add to the main balance.
• There is no time limited over continuous compounding.