Linear Program in Management Accounting

Linear Program is the optimization technique for a system of constraints and a linear objective function. It aims to find the value of the variable that maximizes the objective function. It is the mathematical technique to determine the optimal solution.

In management accounting, the linear program can be used to support management decisions when there are multiple resource limitations. For example, we have limited material and labor which can use to manufacture two product types. There are many combinations of these two products, so we need to use a linear program to calculate a certain level of both products, which can maximize our profit.

Liner program is the alternative technuiqe to analyze the optimal point for company beside of the limiting factor analysis. 

Example of Linear Program

Company A produces product X and Y, which require the following input:

Product	Direct Material	Direct Labor	Selling price
Product X	6 Kg	10 hours	250
Product Y	8 Kg	8 hours	200

The company has a limitation of material and labor as follows:

• Material: 200,000 Kg with a cost of $ 5 per Kg
• Labor: 300,000 hours with a cost of $ 10 per hour

Calculate the amount of products X and Y, which the company needs to produce to maximize the profit.

1. Assume the X and Y is the amount of product X and Y.
2. Define the objective

We are maximizing the contribution, which we assume as the profit.

Contribution of product X & Y:

Product	Selling price/unit (1)	Material cost/unit (2)	Labor /unit (3)	Contribution = (1)-(2)-(3)
Product X	250	(6 Kg * $ 5)	(10 h * $ 10)	$ 120
Product Y	200	(8 Kg * $ 5)	(8 h * $ 10)	$ 80

Total contribution

Contribution = ($ 120 * X) + ($80 * Y)

C = 120X + 80Y

1. Define Constraints

• 6X + 10Y £ 300,000 (limitation of direct material)
• 8X + 8Y £ 320,000 (limitation of direct labor)

X & Y must be greater or equal to zero, and we cannot produce a negative number.

2. Solve the constraint

• Direct material

If X = 0, Y = 30,000

If Y = 0, X = 50,000

• Direct Labor

If X = 0, Y = 40,000

If Y = 0, X = 40,000

3. Build the graph

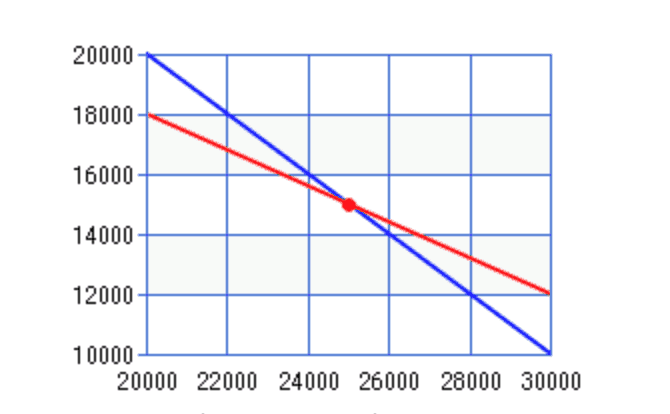
The OABC is the feasible region.

The optimal point is X = 25,000 units and Y = 15,000 units that generate the contribution of $ 4,200,000 [($ 120 * 25,000) + ($ 80 * 15,000)]